Sss sas asa aas and hl congruence worksheet answers – Embark on a journey to conquer the intricacies of SSS, SAS, ASA, AAS, and HL congruence. Delve into the fundamental concepts, explore practical applications, and unravel the mysteries of triangle congruence, unlocking a world of geometric precision.
Our exploration will delve into the very essence of congruence, unraveling the intricacies of SSS, SAS, ASA, AAS, and HL congruence theorems. We’ll equip you with a comprehensive understanding of these concepts, empowering you to tackle congruence problems with confidence and finesse.
Understanding SSS, SAS, ASA, AAS, and HL Congruence: Sss Sas Asa Aas And Hl Congruence Worksheet Answers
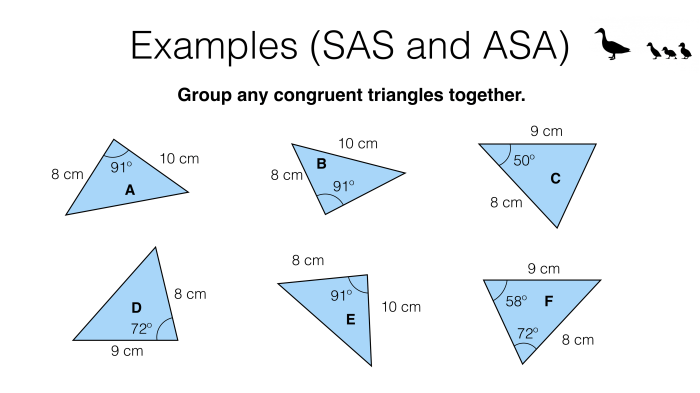
Congruence in triangles refers to the equality of their corresponding sides and angles. In other words, congruent triangles have the same shape and size.
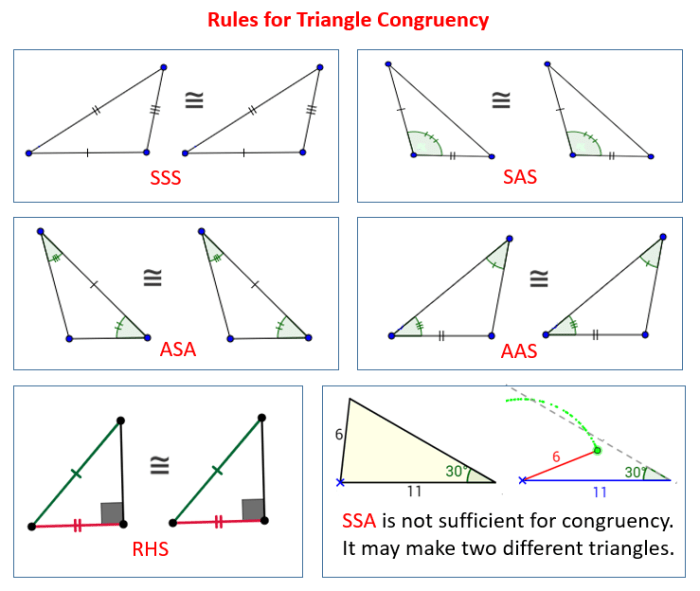
SSS (Side-Side-Side) Congruence: If the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent.
SAS (Side-Angle-Side) Congruence: If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
ASA (Angle-Side-Angle) Congruence: If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
AAS (Angle-Angle-Side) Congruence: If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.
HL (Hypotenuse-Leg) Congruence: If the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the triangles are congruent.
Solving Congruence Problems
To solve congruence problems, follow these steps:
- Identify the given information and what needs to be proven.
- Determine which congruence theorem applies based on the given information.
- State the congruence theorem and justify its use.
- Write the congruence statement and conclude that the triangles are congruent.
Congruence Theorems Table:
| Theorem | Steps |
|---|---|
| SSS | Compare all three sides of both triangles. |
| SAS | Compare two sides and the included angle of both triangles. |
| ASA | Compare two angles and the included side of both triangles. |
| AAS | Compare two angles and a non-included side of both triangles. |
| HL | Compare the hypotenuse and one leg of both right triangles. |
Proving Triangle Congruence
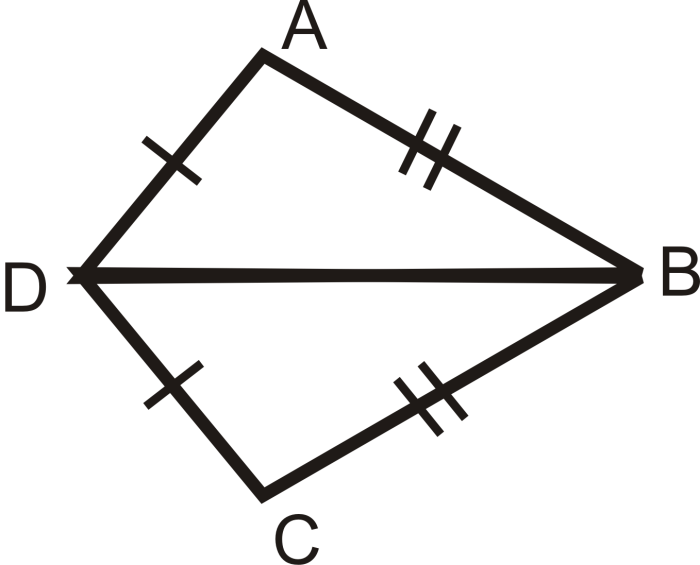
To prove triangle congruence, use the following methods:
- SSS Postulate:If the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent.
- SAS Theorem:If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
- ASA Theorem:If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
- AAS Theorem:If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.
- HL Theorem:If the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the triangles are congruent.
Example:
Prove that triangle ABC is congruent to triangle DEF given that AB = DE, BC = EF, and ∠B = ∠E.
Proof:
By the SAS Theorem, if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
In this case, AB = DE, BC = EF, and ∠B = ∠E.
Therefore, by the SAS Theorem, triangle ABC is congruent to triangle DEF.
Applications of Triangle Congruence
Triangle congruence has various applications in different fields:
- Architecture:Ensuring symmetry and structural stability in buildings and bridges.
- Engineering:Designing bridges, airplanes, and other structures that require precise measurements and shapes.
- Design:Creating aesthetically pleasing and functional designs in furniture, clothing, and artwork.
Example:
In architecture, triangle congruence is used to ensure that the two sides of a building are symmetrical and have the same shape and size. This is important for both aesthetic reasons and structural stability.
FAQ Guide
What is the difference between SSS and SAS congruence?
SSS congruence requires all three sides of two triangles to be equal, while SAS congruence requires only two sides and the included angle to be equal.
How do I prove triangle congruence using the HL theorem?
To prove triangle congruence using the HL theorem, you need to show that the hypotenuse and one leg of one triangle are equal to the hypotenuse and one leg of another triangle.
Can I use AAS congruence to prove that two triangles are similar?
No, AAS congruence cannot be used to prove that two triangles are similar. To prove similarity, you need to use the AA or SSS similarity theorems.