What is the quotient 3y 2 3y – What is the quotient 3y^2 / 3y? Embark on a mathematical expedition to unravel the mysteries of polynomial division and discover the significance of the quotient. From everyday examples to advanced techniques like synthetic division, this exploration unveils the fascinating world of quotients.

Dive into the realm of polynomial division, where we dissect the process step-by-step. Long division takes center stage, revealing its intricacies, while the Remainder Theorem emerges as a guiding light, illuminating the path to understanding remainders.

Quotient Definition: What Is The Quotient 3y 2 3y

In mathematics, a quotient is the result of dividing one number by another. It is often represented by the symbol “÷” or the fraction bar “/”. For example, the quotient of 10 divided by 2 is 5, which can be written as 10 ÷ 2 = 5 or 10/2 = 5.

Quotients in Everyday Situations

Quotients are used in a wide variety of everyday situations. For example, you might use a quotient to:

• Calculate the average of a set of numbers.
• Determine the speed of a moving object.
• Convert between different units of measurement.
• Calculate the cost per unit of a product.
• Divide a pizza equally among a group of friends.

Dividing Polynomials

Polynomials can be divided using a process similar to long division of numbers. This process, known as polynomial long division, allows us to determine the quotient and remainder when one polynomial is divided by another.

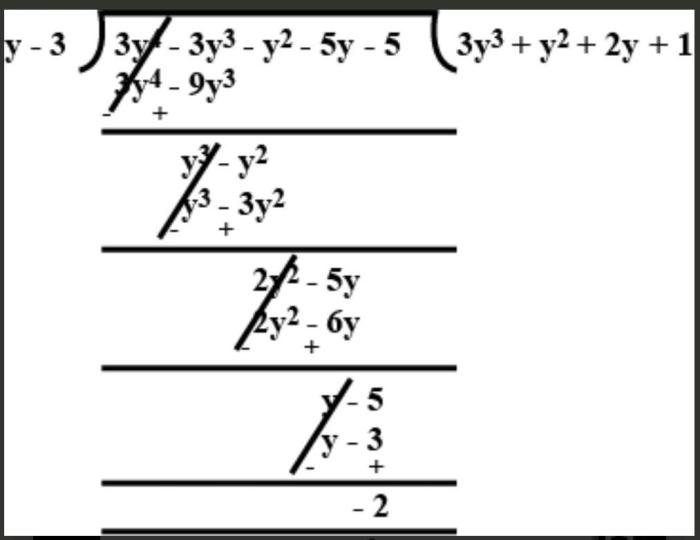
When we divide 3y ²by 3y, we get y. This is a simple algebraic operation. Similarly, when we read the poem To Lucasta, Going to the Wars , we can divide the complexities of war and love into simpler emotions and thoughts, making it easier to understand the human experience.

Long Division of Polynomials

To perform polynomial long division, follow these steps:

1. Arrange the polynomials in descending order of their degrees.
2. Divide the first term of the dividend by the first term of the divisor.
3. Multiply the divisor by the quotient obtained in step 2.
4. Subtract the result from the dividend.
5. Bring down the next term of the dividend.
6. Repeat steps 2-5 until there are no more terms in the dividend.

The quotient is the polynomial obtained from the steps above, and the remainder is the polynomial that remains after all the terms have been divided.

Example

Dividend	Divisor	Quotient	Remainder
3y2 + 5y 2	y 1	3y + 2	0
x3 2x 2+ x 1	x 1	x2 x + 1	0
2x3+ 3x 2 5x + 1	x + 1	2x2+ x 5	6

Remainder Theorem

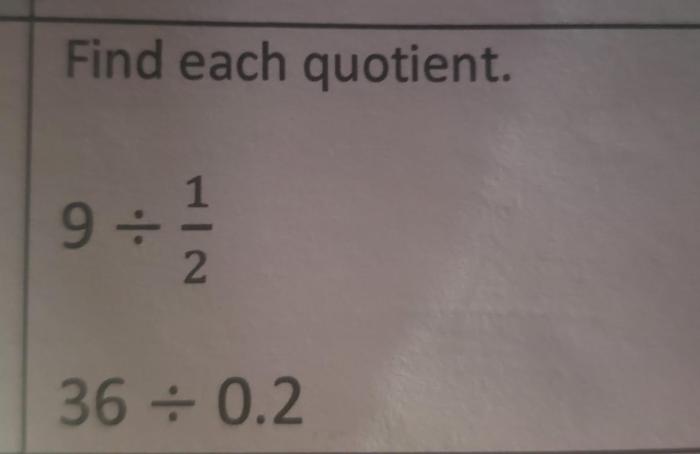
The Remainder Theorem states that when a polynomial f(x) is divided by (xa), the remainder is equal to f(a). In other words, when you plug in the value of a into the polynomial, the result is the remainder of the division.This

theorem is useful in polynomial division because it allows us to find the remainder without actually performing the division. This can be helpful when the polynomial is large or complex.

Example

To find the remainder when f(x) = x^3

• 2x^2 + x
• 1 is divided by (x

1), we can use the Remainder Theorem

f(1) = (1)^3

• 2(1)^2 + (1)
• 1

f(1) = 1

• 2 + 1
• 1

f(1) = 0Therefore, the remainder when f(x) is divided by (x

1) is 0.

Synthetic Division

Synthetic division is a shortcut method for dividing a polynomial by a binomial of the form (xa). It is a more efficient and less error-prone method than long division, especially when the divisor is a simple binomial.

Advantages of Synthetic Division over Long Division

• Fewer steps involved, making it faster.
• Less chance of making errors.
• Easier to check your work.

Table Comparing Synthetic Division and Long Division, What is the quotient 3y 2 3y

| Feature | Synthetic Division | Long Division ||—|—|—|| Number of steps | Fewer | More || Chance of error | Less | More || Ease of checking work | Easier | Harder |

Query Resolution

What is a quotient?

In mathematics, a quotient represents the result of dividing one number by another.

How do I find the quotient of 3y^2 / 3y?

Simplify the expression by canceling out the common factor of 3y, resulting in a quotient of y.